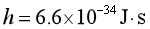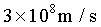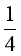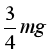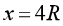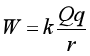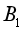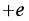(1)a.求放出一个波长为630nm的红色光子时,氧原子的能量变化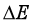 (结果取1位有效数字);
(结果取1位有效数字);
b.请说明带电粒子和空气分子碰撞产生辐射的过程中能量是如何转化的。
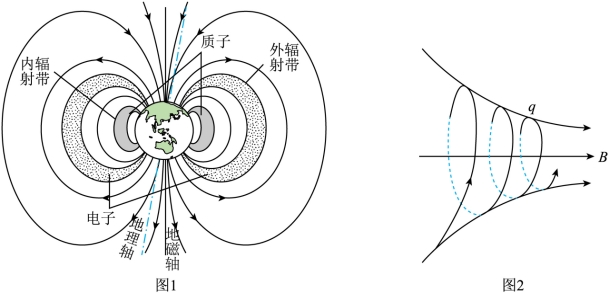
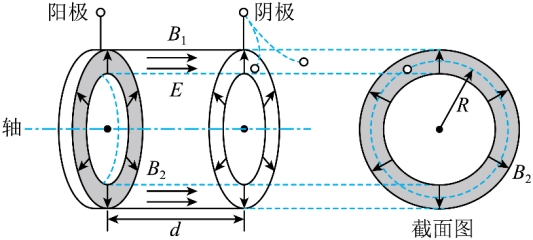
(2)图2所示的是质量为m、电荷量为q的带电粒子在具有轴对称性的非均匀磁场中做螺线运动的示意图,若将粒子沿轴线方向的分速度用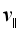 表示,与之垂直的平面内的分速度用
表示,与之垂直的平面内的分速度用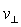 表示。
表示。
a.某时刻带电粒子的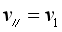 ,
,![]() ,所在处磁感应强度大小为B,如果将粒子从此刻起在垂直平面内做圆周运动的一个周期时间内,所到达区域的磁场按匀强磁场(方向沿轴线)进行估算,求粒子在垂直平面内做圆周运动的半径r和在一个周期时间内沿轴线前进的距离(螺距)d;
,所在处磁感应强度大小为B,如果将粒子从此刻起在垂直平面内做圆周运动的一个周期时间内,所到达区域的磁场按匀强磁场(方向沿轴线)进行估算,求粒子在垂直平面内做圆周运动的半径r和在一个周期时间内沿轴线前进的距离(螺距)d;
b.实际上带电粒子的半径和螺距都会不断变化,已知带电粒子在从弱磁场区向强磁场区运动的同时,在垂直平面内的速度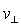 会变大,在此已知的基础上请用高中物理的知识解释为什么带电粒子在从弱磁场区向强磁场区螺旋前进时,分速度
会变大,在此已知的基础上请用高中物理的知识解释为什么带电粒子在从弱磁场区向强磁场区螺旋前进时,分速度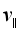 会减小到零,并继而沿反方向前进。
会减小到零,并继而沿反方向前进。
...
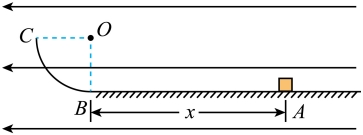
(1)滑块到达B点时的速度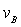 ;
;
(2)滑块在圆弧轨道上运动时,重力和电场力合力的大小和方向;
(3)滑块到达与圆心O等高的C点时,轨道对滑块的作用力大小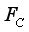 。
。
...
(1)若已知电子运行在半径为r1的轨道上,请根据玻尔原子模型,求电子的动能Ek1及氢原子系统的能级E1。
(2)为了计算玻尔原子模型的这些轨道半径,需要引入额外的假设,即量子化条件。物理学家索末菲提出了“索末菲量子化条件”,它可以表述为:电子绕原子核(可看作静止)做圆周运动的轨道周长为电子物质波波长(电子物质波波长λ与其动量p的关系为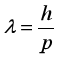 )的整数倍,倍数n即轨道量子数。
)的整数倍,倍数n即轨道量子数。
①请结合索末菲量子化条件,求氢原子轨道量子数为n的轨道半径rn,及其所对应的能级En。
②玻尔的原子模型除了可以解释氢原子的光谱,还可以解释核外只有一个电子的一价氦离子(He+)的光谱。已知氢原子基态的能级为-13.6eV,请计算为使处于基态的He+跃迁到激发态,入射光子所需的最小能量。
...
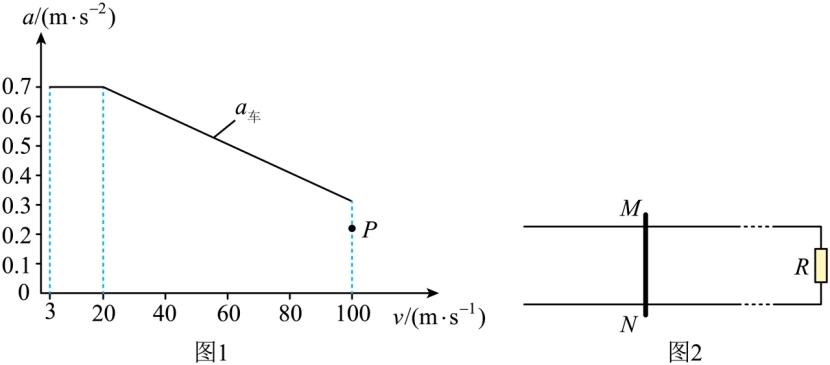
某试验列车按照设定的直线运动模式,利用计算机控制制动装置,实现安全准确地进站停车。制动装置包括电气制动和机械制动两部分。图1所示为该列车在进站停车过程中设定的加速度大小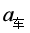 随速度
随速度 的变化曲线。
的变化曲线。
(1)求列车速度从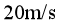 降至
降至![]() 经过的时间t及行进的距离x。(保留1位小数)
经过的时间t及行进的距离x。(保留1位小数)
(2)有关列车电气制动,可以借助图2模型来理解。图中水平平行金属导轨处于竖直方向的匀强磁场中,回路中的电阻阻值为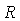 ,不计金属棒
,不计金属棒 及导轨的电阻。
及导轨的电阻。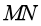 沿导轨向右运动的过程,对应列车的电气制动过程,可假设
沿导轨向右运动的过程,对应列车的电气制动过程,可假设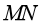 棒运动的速度与列车的速度、棒的加速度与列车电气制动产生的加速度成正比。列车开始制动时,其速度和电气制动产生的加速度大小对应图1中的
棒运动的速度与列车的速度、棒的加速度与列车电气制动产生的加速度成正比。列车开始制动时,其速度和电气制动产生的加速度大小对应图1中的 点。论证电气制动产生的加速度大小随列车速度变化的关系,并在图1中画出图线。
点。论证电气制动产生的加速度大小随列车速度变化的关系,并在图1中画出图线。
(3)制动过程中,除机械制动和电气制动外,列车还会受到随车速减小而减小的空气阻力。分析说明列车从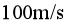 减到
减到![]() 的过程中,在哪个速度附近所需机械制动最强?
的过程中,在哪个速度附近所需机械制动最强?
(注意:解题过程中需要用到、但题目没有给出的物理量,要在解题时做必要的说明)
...
如图甲所示,真空中有一长直细金属导线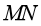 ,与导线同轴放置一半径为
,与导线同轴放置一半径为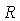 的金属圆柱面。假设导线沿径向均匀射出速率相同的电子,已知电子质量为
的金属圆柱面。假设导线沿径向均匀射出速率相同的电子,已知电子质量为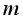 ,电荷量为
,电荷量为 。不考虑出射电子间的相互作用。
。不考虑出射电子间的相互作用。
(1)可以用以下两种实验方案测量出射电子的初速度:
a.在柱面和导线之间,只加恒定电压;
b.在柱面内,只加与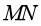 平行的匀强磁场。
平行的匀强磁场。
当电压为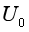 或磁感应强度为
或磁感应强度为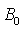 时,刚好没有电子到达柱面。分别计算出射电子的初速度
时,刚好没有电子到达柱面。分别计算出射电子的初速度 。
。
(2)撤去柱面,沿柱面原位置放置一个弧长为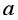 、长度为
、长度为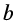 的金属片,如图乙所示。在该金属片上检测到出射电子形成的电流为
的金属片,如图乙所示。在该金属片上检测到出射电子形成的电流为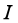 ,电子流对该金属片的压强为
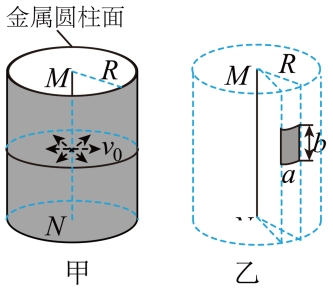
,电子流对该金属片的压强为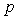 。求单位长度导线单位时间内出射电子的总动能。
。求单位长度导线单位时间内出射电子的总动能。
...
已知电子的质量为m、电荷量为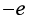 ;对于氙离子,仅考虑电场的作用。
;对于氙离子,仅考虑电场的作用。
(1)求氙离子在放电室内运动的加速度大小a;
(2)求径向磁场的磁感应强度大小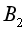 ;
;
(3)设被电离的氙原子数和进入放电室的电子数之比为常数k,单位时间内阴极发射的电子总数为n,求此霍尔推进器获得的推力大小F。
...
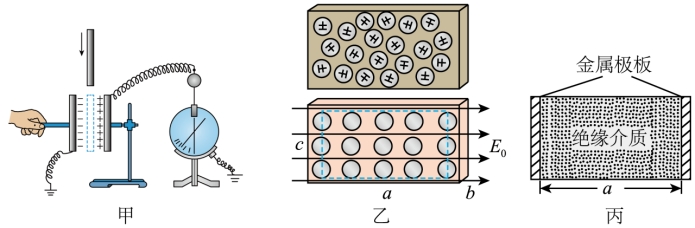
(2)绝缘介质中只有不能自由移动的束缚电子和原子实(带正电)。把绝缘介质放入电场中,由于束缚电子和原子实的电性不同,受到静电力方向不同,因此束缚电子和原子实被“拉开”极小距离,最终的宏观效果为均匀介质表面出现正负电荷,如图乙所示。这种现象称为介质的极化,表面出现的电荷称为极化电荷。
a.现有一长方体均匀绝缘介质,长、宽、高分别为a、b、c,若沿a方向施加场强为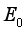 的匀强电场,绝缘介质表面单位面积产生的极化电荷量为P。极化电荷分布在介质表面可视为平行板电容器,电容
的匀强电场,绝缘介质表面单位面积产生的极化电荷量为P。极化电荷分布在介质表面可视为平行板电容器,电容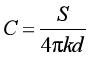 ,k为静电力常量,不考虑边缘效应,求极化电荷产生电场的场强E的大小;
,k为静电力常量,不考虑边缘效应,求极化电荷产生电场的场强E的大小;
b.请根据上述材料,解释(1)中插入绝缘介质(如图丙所示)后电容器的电容变化的原因.(需要的物理量可自行设定)
...
定值电阻、电容器、电感线圈是三种常见的电路元件,关于这几个元件有如下结论:
①一个定值电阻R满足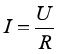 关系;
关系;
②一个电容器的电容为C,两极板间电压为U时,储存的能量为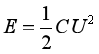 ;
;
③一个电感线圈的自感系数为L,自感电动势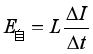 ,式中
,式中![]() 为电流变化率;通过的电流为I时,储存的能量为
为电流变化率;通过的电流为I时,储存的能量为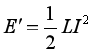 。
。
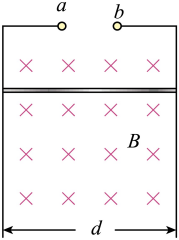
如图所示,足够长的光滑金属框架竖直放置,顶端留有接口a、b,两竖直导轨间距为d。一质量为m、长度为d的金属棒始终与竖直导轨接触良好,磁感应强度为B的匀强磁场与框架平面垂直,重力加速度为g。不计空气阻力,不计框架和金属棒的电阻及电磁辐射的能量损失。
(1)若在a、b间接入一个阻值为R的定值电阻,现从静止释放金属棒,求金属棒的最终速度大小v1;
(2)若在a、b间接入一个电容为C的电容器,现从静止释放金属棒,求当电容器两极板间电压为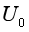 时,金属棒下落的高度h;
时,金属棒下落的高度h;
(3)若在a、b间接入一个电阻不计、自感系数为L的电感线圈,现从静止释放金属棒,求金属棒下落过程中的最大速度v2。
...
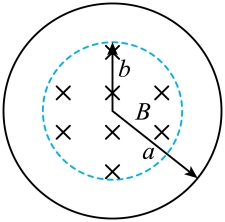
(1)金属圆环内感应电动势的大小E;
(2)金属圆环中感应电流的方向和感应电流的大小I;
(3)金属圆环单位长度上的发热功率P。
...
(提示:不涉及求解半径的问题,圆周运动向心加速度的大小可表示为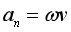 )
)
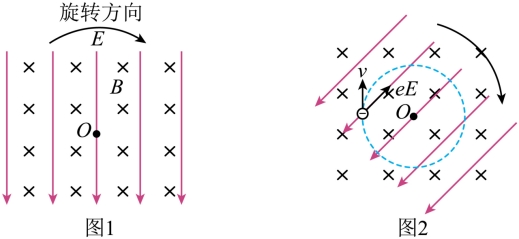
(1)若空间只存在匀强磁场,电子只在洛伦兹力作用下做匀速圆周运动,求电子做圆周运动的角速度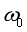 。
。
(2)将电子回旋共振简化为二维运动进行研究。施加旋转电场后,电子在图2所示的平面内运动,电子运动的过程中会受到气体的阻力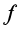 ,其方向与速度
,其方向与速度![]() 的方向相反,大小
的方向相反,大小![]() ,式中k为已知常量。最终电子会以与旋转电场相同的角速度做匀速圆周运动,且电子的线速度与旋转电场力的夹角(小于90°)保持不变。只考虑电子受到的匀强磁场的洛伦兹力、旋转电场的电场力及气体的阻力作用,不考虑电磁波引起的能量变化。
,式中k为已知常量。最终电子会以与旋转电场相同的角速度做匀速圆周运动,且电子的线速度与旋转电场力的夹角(小于90°)保持不变。只考虑电子受到的匀强磁场的洛伦兹力、旋转电场的电场力及气体的阻力作用,不考虑电磁波引起的能量变化。
a.若电场旋转的角速度为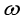 ,求电子最终做匀速圆周运动的线速度大小v;
,求电子最终做匀速圆周运动的线速度大小v;
b.电场旋转的角速度不同,电子最终做匀速圆周运动的线速度大小也不同。求电场旋转的角速度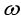 多大时,电子最终做匀速圆周运动的线速度最大,并求最大线速度的大小
多大时,电子最终做匀速圆周运动的线速度最大,并求最大线速度的大小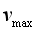 。
。
c.旋转电场对电子做功的功率存在最大值,为使电场力的功率不小于最大功率的一半,电场旋转的角速度应控制在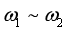 范围内,求
范围内,求![]() 的数值。
的数值。
...
1、本网站所提供的信息,只供教育教学参考之用。
2、本网站及其会员一概毋须以任何方式就任何信息传递或传送的失误、不准确或错误对用户或任何其他人士负任何直接或间接的责任。
3、在法律允许的范围内,本网站在此声明,不承担用户或任何人士就使用或未能使用本网站所提供的信息或任何链接或项目所引致的任何直接、间接、附带、从属、特殊、惩罚性或惩戒性的损害赔偿。
4、访问者在从事与本网站相关的所有行为(包括但不限于访问浏览、利用、转载、宣传介绍)时,必须以善意且谨慎的态度行事;访问者不得故意或者过失的损害本网站的各类合法权益,不得利用本网站以任何方式直接或者间接的从事违反中华人民共和国法律、国际公约以及社会公德的行为。对于访问者利用本网站提供的信息而作出的任何决策、决定以及其后果,本网站不承担任何责任
5、本网站图片,文字之类版权,本网站无法鉴别所上传图片或文字的知识版权,如果侵犯,请及时通知我们,本网站将在第一时间及时删除。
6、凡以任何方式登录本网站或直接、间接使用本网站资料者,视为自愿接受本网站声明的约束。
XueXi Design